Billy Levin

An Introduction to Chess Engine Programming

If you like chess and you like programming, I think you will both enjoy and get a lot of value out of creating your own chess engine. This post is a high-level description of the main topics you’d be likely to encounter when doing so.

Overview

A chess engine can be split into three high-level areas:

  1. Board representation: the engine needs to keep track of where all the pieces are, whose turn it is to move, etc. It also needs to be able to generate all the legal moves in a given position so that they can be analysed

  2. Search: the engine needs to be able to look ahead as far as possible at moves and counter-moves in order to improve the accuracy of the move it eventually decides to play

  3. Evaluation: the engine needs to be able to make sense of a given position and determine which side it benefits and by how much

All three areas have some overlap but they are roughly distinct conceptually and so we will look at them one at a time. In practice, search and evaluation are quite intertwined - changes to evaluation will often require parameters used in search optimisations to be tuned, for example.

I would recommend having an understanding of the main rules of chess ↗ before trying to create your own chess engine, and even before reading the rest of this post.

Part 1: Board Representation

Before the engine can begin to analyse chess positions, it needs to construct an internal representation of them. The key pieces of information about a chess position that a chess engine needs to maintain knowledge of are:

In this post, we will look at how bitboards ↗ are used to store or derive this information, but there are other ways to represent a chess board ↗.

Bitboards

It is a fortunate coincidence that a chess board has 64 squares, and that modern computers can perform operations on 64-bit integers efficiently. Many chess engines take advantage of this fact to embed the placement of pieces on the board inside an integer, with each bit representing the occupancy of a single square. This is called a bitboard.

Since each bit acts as a boolean (a piece is here, or a piece is not here), we cannot represent every piece using a single bitboard. Instead, we have to maintain 12 bitboards - one for each piece type (pawn, knight, bishop, rook, queen, king) for each colour (white, black).

The decision we make on which bits represent which squares will affect how we write the bitwise operations for adding/removing pieces and generating possible moves. One example is little-endian rank-file (LERF) mapping, which starts with the A1 square at index 0 (rightmost bit) and ends with H8 at index 63 (leftmost bit). The below image portrays how the indices line up if you’re looking at a chess board from white’s perspective:

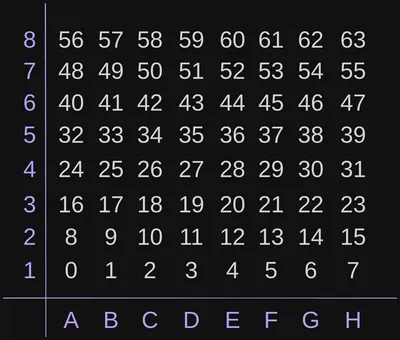
visual representation of a little-endian rank-file mapping bitboard. A1 is index 0, B1 is index 1, etc. ending with H8 at index 63

When written down as a binary number, it would look like this, with H8 as the leftmost bit and A1 as the rightmost bit: H8G8F8E8D8C8B8A8H7…A1

All examples in this post will use LERF.

Here are some bitwise operations that are commonly used when working with bitboards:

Position Parsing

Chess engines need to be able to construct a board representation for different positions as the game progresses. The standard way to do this is by parsing a string that will be provided in Forsyth-Edwards Notation ↗ (FEN). FEN provides a snapshot of the current state of the board, without much information about what happened in the game previously. You can extract the following information from a FEN string:

  1. Piece placement
  2. Side to move
  3. Castling rights
  4. En passant ↗ square
  5. Halfmove clock: used to keep track of progress towards the fifty-move rule. This is measured in halfmoves (a move made by one side), and so the clock would need to be at 100 for the fity-move rule to be met. This clock gets reset whenever a piece is captured or a pawn is moved
  6. Fullmove clock: increments each time both players make a move

I would strongly recommend implementing a way to print your board representation before doing this - it makes debugging a lot easier. I like to use the chess piece unicode symbols ↗ to print something that looks like a proper chess board.

screenshot of a printed chess board

Move Generation

It is crucial that a chess engine is aware of every possible legal move in a given position. If using bitboards, moves can be generated using combinations of bit shifts depending on the type of piece being moved. Here are some useful operations (the directions assume you are looking at the board from white’s perspective):

NOT_A_FILE and NOT_H_FILE are bit masks that ensure a piece doesn’t spill over to the opposite side of the board (e.g. a piece on the A file should not end up on the H file if it attempts to go west). The bit mask has each bit set to 1 except for the bits that correspond to its file.

As an example, if you wanted to generate a possible north-north-east move for a knight, you could combine the shifts like so: north_north_east = (bitboard << 17) & NOT_A_FILE

These bitboards can be precomputed for each square and looked up at runtime.

Note that this only generates possible moves. To determine which moves can actually be made, the engine typically also keeps “occupancy” bitboards for each side. These are bitboards where if any piece of the particular side is on that square, the bit is set to 1, and 0 otherwise. To illustrate why this is necessary, imagine a knight on D5 that wants to jump to E7. There are three possibilities:

  1. The square is empty: the knight can jump there
  2. The square is occupied by a friendly piece: the knight cannot jump there
  3. The square is occupied by an enemy piece: the knight can jump there and captures the piece

To perform these checks, we can make use of the occupancy bitboards:

The situation is more complicated for the so-called “sliding pieces” (bishops, rooks, queens) because they can move indefinitely in a given direction until being blocked by either a piece or the edge of the board. For this reason, we cannot simply precompute bitboards for each square like we can do for knights or kings or pawns, since more information is needed about the current state of the board (i.e. the placement of all the pieces). “Magic bitboards” is an efficient technique to map a square and occupancy bitboard to a precomputed attack bitboard. How they work is out of the scope of this post, but check out these links for more information:

Make and Unmake Moves

In order to search the game tree more deeply than just the current position, the engine needs to internally “make” and “unmake” moves, updating the board representation so that it can analyse positions that may occur in the future.

Here are some things that typically need to be updated when making a move:

When unmaking a move, there are some aspects of the position that are not directly reversible. For example, previous castling rights cannot be determined just by knowing what move was made. In order to correctly unmake a move, we can maintain a history of any irreversible state when making a move, then read and apply it when unmaking the move.

Perft

When implementing move generation, it’s easy to overlook certain types of moves or get them wrong. The best way to verify that an engine’s move generation is correct is to run a perft ↗ (short for performance test) suite on lots of different positions. Despite its name, perft is mostly a test of correctness rather than performance.

Perft is a function that searches a position to a particular depth and counts the total number of possible legal moves. This number is then compared to the expected total. If it matches, then it’s extremely likely that move generation is correct.

The test data is provided in Extended Position Description ↗ (EPD) format, which is pretty much just a FEN with some additional data (in the case of perft, depth and expected node count) attached. EPD files with test positions produced by the community can be found online.

Once the engine has a correct board representation and can make/unmake moves, it’s ready to start searching for good moves to play. We can model all the possible positions as a game tree ↗, where the tree nodes are chess positions and the branches are moves. The player to move switches at each level of the tree. Each level (a move by one side) is known as a “ply”. I’ll use “ply” and “depth” interchangeably in this post. Generally speaking, the best search algorithm is one that can traverse the game tree as deeply as possible in a given timeframe (games of chess usually have a time limit, plus it’s impossible to search every move until game completion even with infinite time).

Minimax

One popular algorithm for traversing the game tree is minimax ↗. In the context of chess, minimax is a depth-first search of the tree, with the key assumption being that each player will do what is best for themselves and worst for their opponent, and that each player is aware that their opponent will do this. This works because chess is a zero-sum game - what is good for one player is equally bad for the other.

Let’s look at a simple example. In the diagram below, it’s white to move. They are deciding between move A and move B. The values in the terminal nodes are the result of an evaluation of the position - assume that a positive number is good for white and a negative number is good for black (with these assumptions, we say that white is the “maximising” player in the context of minimax).

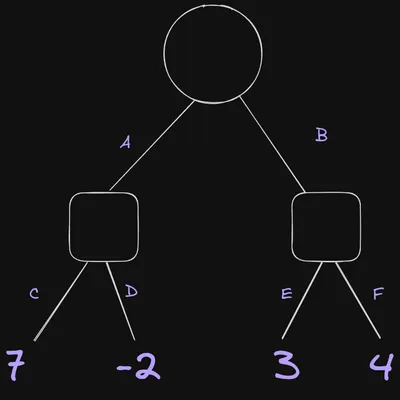
game tree, the root has two branches - move A and move B. after move A, there are two more branches - move C and move D. move C terminates with value 7, while move D terminates with value -2. going back to move B, that also has two branches - move E and move F. move E terminates with value 3, while move F terminates with value 4

Here is how the traversal would go:

  1. White to move: Make move A
  2. Black to move: Make move C
  3. Evaluation after move C is 7
  4. Unmake move C
  5. Black to move: make move D
  6. Evaluation after move D is -2. This is better for black than 7, so that is the move they will pick. The value of the game tree after move A is -2
  7. Unmake move D
  8. Unmake move A
  9. White to move: make move B
  10. Black to move: make move E
  11. Evaluation after move E is 3
  12. Unmake move E
  13. Black to move: make move F
  14. Evaluation after move F is 4. This is worse for black than 3, so black will not pick move F in this position. The value of the game tree after move B is 3
  15. Unmake move F
  16. Unmake move B
  17. White picks move B because its value is higher than move A
  18. The final value of the position is 3

Note that the actual best case scenario for white in this position is move A followed by move C which gives a value of 7. However, this is disregarded by the algorithm because we assume that black won’t allow that to happen.

In order to implement minimax, an evaluation function is needed. A simple function that counts and compares the total piece values ↗ for both sides will suffice for now. We’ll look at improvements to evaluation later.

Minimax is most commonly implemented as negamax ↗. This has the exact same behaviour as minimax but the code is simpler. Negamax requires the evaluation function to provide the score relative to the current player - in other words, if the current side to move is winning, it returns a high score, and a low score if they’re losing. This differs from minimax where the score would be high if the maximising player is winning and low if the minimising player is winning.

Alpha-Beta Pruning

While minimax is a reliable way to find good moves, it requires visits to every node in the tree. This means it’s too slow. Fortunately, there are ways to reduce the number of nodes visited. This is what most search optimisations aim to achieve - fewer node visits without accidentally missing good moves.

Probably the most effective of these optimisations is alpha-beta pruning ↗. This is a pure enhancement to minimax - it is guaranteed to produce the exact same result as regular minimax, but with opportunities to prune (i.e. stop searching the descendants of) some branches.

Alpha-beta introduces a lower (alpha) and upper (beta) bound to the value of the tree. These bounds are used to prove that certain moves will not affect the search outcome, and so can be pruned from the tree.

Alpha-beta visits the fewest nodes when the first move it checks is the best move. Therefore, to get the best performance out of it, we try to order our moves ↗ (more on this in the next section) so that we search moves that are most likely to be good early on. More on this in the next section.

We won’t go into the details of the algorithm implementation here, but let’s see intuitively how it works. I’ve modified the game tree we looked at earlier slightly so that now move A is the better move:

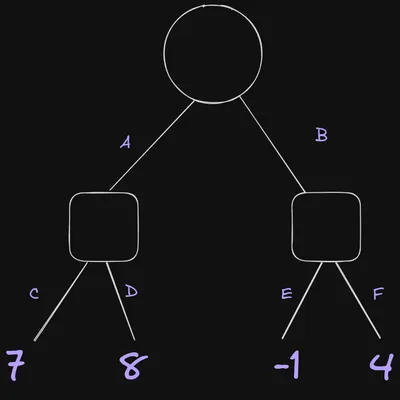
game tree, the root has two branches - move A and move B. after move A, there are two more branches - move C and move D. move C terminates with value 7, while move D terminates with value 8. going back to move B, that also has two branches - move E and move F. move E terminates with value -1, while move F terminates with value 4

The tree is traversed in the same way as before, but let’s pause when we get to move E. At this point, we already know that move A will provide a minimum score of 7. But move E gives a score of -1, which is better for black. The fact that black has the opportunity here to play a move that’s worse for white than any option in the “move A” branch means it is pointless to search any further - white has no reason to pick move B over move A. Therefore, we can prune the remaining children of move B (in this example, that’s just move F). Move F could have a score of 10,000 and it wouldn’t matter because we wouldn’t expect black to pick it over move E.

Move Ordering

As mentioned, good move ordering is crucial to maximise the efficiency of alpha-beta search. Searching best moves earlier == more cutoffs == fewer positions to look at == deeper searches in the same amount of time.

There are two types of move that are pretty much always prioritised during search:

  1. The previous best move - if a move was judged to be best at a lower ply, it’s likely to still be the best now
  2. Captures - also often likely to be good moves, either through winning material or refuting an opponent’s move. Usually captures of higher-value pieces are checked first, i.e. prioritise moves that capture a queen over those that capture a pawn

There are other move ordering mechanisms that tend to improve the quality of search, most notably the killer heuristic ↗ and history heuristic ↗. Many engines also include pawn promotions in the search hierarchy. What’s been mentioned here is not exhaustive and there are plenty of mechanisms to experiment with ↗ (or indeed try out your own ideas!).

Quiescence

A frequent problem that chess engines run into is the horizon effect ↗, which occurs when the nature of the position would drastically change if it was searched more deeply. Imagine a queen trade was initiated by one player by capturing their opponent’s queen with their own. On the next turn, the opponent will almost certainly capture the queen back to retain material balance. However, the engine wasn’t programmed to search deeply enough to see the recapture. The engine would incorrectly evaluate that one side has a massive material advantage because they still have their queen while their opponent doesn’t. This is the horizon effect.

Quiescence search is one of several ways we can attempt to mitigate the horizon effect. It ensures that even if the engine hits its depth limit, it keeps searching until the position is “quiet” - usually meaning there are no captures available. To make it practical to carry out this search within a reasonable amount of time, the search is usually a lot simpler than the main search function and it only searches moves that are captures.

There are several other search extensions ↗ that can be experimented with to further diminish the horizon effect.

Transposition Table

While searching, the engine frequently encounters the same position via different move orders. This is known as a transposition. We can store the results of searches on positions in a hash table and then look them up if we reach them again in a different path of the search, potentially saving a lot of time. We call that hash table a transposition table ↗.

Since a transposition table is a hash table, we need a way to hash a chess position. The most common method is Zobrist Hashing ↗. Let’s see how it works.

To begin, we need to generate a random number for each possible important aspect of the position. For example:

This totals 794 random numbers that need to be generated.

The hashing function is pretty simple - any time an aspect of the position changes, we apply the bitwise XOR operation to the hash and the corresponding random number for the detail that changed.

For example, if we moved a white knight from D5 to E7, it would look something like this:

hash ^= white_knight_d5_hash ^ white_knight_e7_hash

(where ^ is XOR and white_knight_{square}_hash is the randomly generated number that corresponds to the white knight on the given square)

This hashing method works for transpositions because XOR is self-inverting, i.e. a ^ b ^ b == a. So, if we were to move the knight back to D5 from E7 (hash ^= white_knight_e7_hash ^ white_knight_d5_hash), the hash value would be back to the same as it was originally.

If a transposition table has been used, it can implicitly cover the “previous best move” case in move ordering if we compare the current move to the move stored in the transposition table for the current position.

Transposition tables can also be used to speed up perft by storing the node counts for a particular position at a particular depth.

Time Management

Most games of chess have some kind of time control. In a timed game, a chess engine needs to resolve two issues:

  1. How long should it spend searching for a move?
  2. How can it predict what ply it’ll be able to search to within the allocated timeframe?

The first question is quite trivial. When playing a game the engine will be provided useful information for managing time, such as:

We can use this information to allocate a time limit for each move. A basic formula might look like this:

allocated_time = (time_left / moves_to_go) + increment

Then we can periodically check if the allocated time is up and break out of the search if it is.

There are more sophisticated adjustments that can be made to this, such as spending less time on moves earlier in the game where positions are usually less critical.

The second question is a lot more complicated. We don’t know in advance how many nodes we’ll need to visit. We could maybe make guesses about the expected branching factor ↗ of a position and use that to estimate how deeply our engine will be able to search, but it’s bound to be wrong often.

Fortunately, there’s a great solution to the second question called iterative deepening ↗. The way it works is it carries out a depth-first search at depth 1, then at depth 2, etc. until the allocated time has been used. Imagine this process has repeated to depth 5 but then time runs out before the search at depth 6 is complete. We are able to fall back to the best move we found at depth 5 (assuming we’ve saved it somewhere). This approach requires no upfront guesswork about how long a search will take.

At first glance, iterative deepening seems inefficient since we’re repeating searches on each iteration. However, since the number of nodes visited grows exponentially, the vast majority of the work will always be done on the highest depth we reach. Let’s illustrate this. It’s thought that an average chess position has a branching factor of around 35. That means for a search at depth d, we’ll visit around 35d nodes. Here’s a table that displays the node count for each depth up to 7:

Depth Average nodes visited
1 35
2 1225
3 42,875
4 1,500,625
5 52,521,875
6 1,838,265,625
7 64,339,296,875

As we can see, for a given depth d, the total nodes visited is far greater than those from depth 1 to d-1 combined. As the depth increases, the impact of repeated searches diminishes further.

But Wait, There’s More

The concepts we’ve looked at in this section are not exhaustive. There are many more enhancements that can be made to alpha-beta that we haven’t discussed. I chose to talk about what are probably the most commonly used optimisations across most engines. On their own, they are enough to play a decent game of chess.

Here are some more (still not exhaustive) enhancements to look at:

Part 3: Evaluation

Any effort put into optimising search will be wasted if the engine doesn’t have a good evaluation function to match. Evaluation is where engines most diverge in their implementation and where the author can be most creative.

The evaluation function assigns a given position a numerical value that describes which side has an advantage and by how much. This score is typically measured in centipawns, defined as 1/100 the value of a pawn.

Recall from the minimax section that the evaluation function has to be implemented differently depending on whether minimax or the more common negamax is used. In minimax the score is relative to the maximising player, whereas in negamax it’s relative to the player that’s currently making a move in the position. Assuming the maximising player is white and that white is winning by three pawns, here’s a table illustrating the differences in output of evaluation:

Side to move Minimax Negamax
White 300 300
Black 300 -300

Let’s look at some considerations an evaluation function might make, starting with the most important: material.

Material

In any position that isn’t a forced checkmate, material is the dominating factor in evaluation. The relative value of the pieces is one of the first things a new chess player learns and its importance remains true for engines.

While the standard piece values will work well, tweaking these values is common ↗.

We know from playing chess that pieces can be more or less valuable than their base value depending on the current state of the game. Most evaluation heuristics aim to recognise these different factors and apply bonuses/reductions to piece values where appropriate.

Piece-Square Tables

There is general wisdom in chess about where certain pieces tend to “belong” on the chess board. For example, usually you want pawns and pieces to be occupying or controlling the centre of the board in the early and middle stages of the game, while in the endgame your goal tends to revolve around marching pawns up the board to try and promote them. These general rules can be represented in a data structure called a piece-square table ↗. A piece-square table, unsurprisingly, maps a piece and a square to a value representing either a bonus or a penalty for that piece. For example, a knight on D5 might be given a bonus of 20 centipawns, while a knight on H5 is given a penalty of -10 centipawns since, generally speaking, knights are better in the centre than they are on the edge.

It’s beneficial to have two different tables for each piece - one for the early/middlegame and one for the endgame. This is especially important for pawns since their purpose becomes radically different as the number of pieces on the board decreases.

Piece Mobility

Another property that can impact a piece’s value is how mobile it is, or in other words, how many squares it’s able to move to. A bishop that has access to a full open diagonal will usually be more valuable than one that only has a couple of squares available to it, for example.

The simplest implementation of this would be to give a bonus to each piece that equals the number of moves it can make. However, there’s room for experimentation here. Perhaps certain pieces should have a multiplier that compounds the value for each additional square it can move to, or maybe the mobility of a certain piece could be more valuable in the endgame.

Tapered evaluation

While distinguishing between the middlegame and endgame in evaluation is valuable, it has a flaw. At some point, a piece is going to be captured and the engine is going to determine that the game has transitioned into the endgame, potentially causing a big change in its evaluation. This discontinuity in evaluation suggests that the evaluation isn’t as accurate as it could be.

This issue can be mitigated with a technique called tapered evaluation ↗. It works by smoothly transitioning between the middlegame and endgame evaluations as pieces are removed from the board. You can think of it like a gradient - with lots of pieces on the board, the evaluation will heavily favour the middlegame evaluation heuristics, but as more and more pieces are captured, the evaluation gives more and more weight to the endgame heuristics.

tapered evaluation representation. a gradient between middle and endgame with the current position being somewhere in between

Draw Detection

Being able to detect a drawn position is important so that the engine doesn’t accidentally stumble into a draw when it thinks it’s winning. Imagine the engine is ahead in material and believes it has a strong advantage over its opponent. It could unknowingly pick a drawing move in the following situations:

All of these draw conditions should be checked during evaluation, producing a value of zero if any are met.

There are also positions which are “drawish”, meaning that they aren’t legally a draw but it’s very likely that a draw will occur. An example of this is King and Two Knights vs King. The side with two knights has a large material advantage but it’s not possible to forcibly checkmate the enemy king. However, with poor play by the side with only the king, it is technically possible to be checkmated and so the position isn’t legally declared a draw. It’s a good idea to handle these situations also, either by evaluating it as a draw or scaling the score down to reflect the fact that it’s likely to be a draw.

But Wait, There’s More Again

Like with search, there’s a lot more that can (and should) be done with evaluation. This is where you can really make your engine your own. The concepts we’ve spoken about will allow an engine to play a good game of chess, but it’ll still be prone to misevaluation and blunders.

Many of the considerations that humans make when evaluating chess positions can also be made by engines. Here are a few examples of traditional human evaluation criteria that wouldn’t be out of place in a chess engine’s evalaution:

Be creative and experiment!

Wrapping Up

There’s a couple more things to talk about that don’t fit into a specific section.

Communication

In order to play against other engines (or even humans), your engine needs a way to communicate with whatever software the game is running on. In the context of a standard game of chess, the communcation protocol is used to provide the engine with information on the current position, including:

The engine will use this information to determine the move it would like to play, and sends that information back to the GUI/CLI/whatever it is communicating with.

The two most common communication protocols are the Universal Chess Interface ↗ (UCI) and the Chess Engine Communication Protocol ↗ (often referred to using its corresponding GUIs WinBoard and XBoard).

UCI is the most popular. Make sure to implement a protocol that’s compatible with whatever software you’re using, whether that be for your own testing or for a match/tournament. I like to use the Cute Chess ↗ CLI and GUI for testing.

Playing Strength

When making changes to your engine, you will want to make sure that its playing strength hasn’t weakened - and ideally that it’s become stronger, of course. The best way to measure the strength of an engine is to see how it performs in real games.

For simplicity, you can be relatively confident that your engine has improved if it performs well against the previous version of itself. However, this has the potential pitfall that you’re training your engine to beat itself rather than to be good at chess generally. For this reason, if you’re serious about creating a strong engine, you should be testing it against other engines ↗.

If you want to get a more accurate understanding of how strong your engine is, you can get an elo rating via the Computer Chess Rating Lists ↗ (CCRL).

What Now?

If you’d like to create your own chess engine, here are some resources for further learning and guidance. It’s a bit of a rabbit hole, so I’d recommend getting started on your own implementation as early as possible and then looking things up to unblock yourself rather than overwhelming yourself with information from the start. Anyway, here are the resources:

Thanks for reading if you got this far. I hope this post will be useful to refer back to when trying to solidify your understanding of this small subset of chess programming topics.

If you do create an engine, please share it with me! I’d love to take a look.